|
출처 : dreamhack.io |
동아리에서 암호학을 공부할 기회가 생겨서 드림핵보고 공부한 것을 정리해보려고 한다.
1. 개요
- 대칭키 암호 : 암호화와 복호화에 같은 키를 쓰는 알고리즘
-> 전제 조건 : 수신자와 송신자가 같은 키를 공유하고 있어야 함 - 대칭키 암호 시스템을 사용하여 통신하려면, 데이터를 교환하기 전에 키 교환(Key Exchange)이 이뤄져야 함
- 하지만 일반적으로 아주 먼 거리의 대상과 통신하는 현대 유무선 환경에서는 안전한 키 교환이 쉽지 않음
- 공개된 채널을 통해 키를 교환해도 외부인은 키를 알 수 없게 하는 공개 키 교환 알고리즘 등장!
2. 수학적 원리
전 이거 완벽하게 이해 못했습니다.
1) 모듈로 연산에서의 거듭제곱
임의의 합동 항등식에 대해, 양변에 동일한 값을 곱해도 식은 성립한다.

위를 이용하여 큰 지수에 대한 합동식을 빠르게 연산하는 알고리즘을 squeare and multiply라고 한다.

Diffie-Hellman 키 교환 알고리즘을 사용하려면 2048번 가까이 제곱된 어떤 수의 모듈러 값을 구해야 하는데, 이 방법을 사용하면 2048번 정도만 연산해도 그 값을 구할 수 있다. ? ??
2) 페르마의 소정리

예시)
소수 37과 2, 3, 17 대입 해보면 됨. 물론 난 계산 안해봄 ㅎ..
2^36 == 3^36 == 17^36 == 1 (mod 37)
3) 이산 로그 문제

예시)

만약 m이 엄청 커진다면?
식이 성립하는 x를 무차별 대입으로 찾기가 매우 어렵다.
Diffie-Hellman 알고리즘의 안전성은 이산 로그 문제의 어려움에 바탕을 두고 있다.
Diffie-Hellman 키 교환 알고리즘에서 키를 모르는 공격자가 키를 구하려면 m이 2^2048정도 되는 이산 로그 문제를 풀어야 한다.. 이는 현재의 연산능력으로 불가능하다고 한다.
3. Diffie-Hellman 키 교환
- 최초의 공개 키 교환 알고리즘
- 현재도 널리 사용되고 있음!!!
등장인물 : Alice, Bob

Alice가 먼저 소수 p와 1<=g<=p-1을 만족하는 적당한 수 g를 정해 Bob에게 전송한다.
(소수 p는 보통 2^1024 이상의 큰 수)
다시 Alice는 1<=a<=p-1을 만족하는 적당한 수 a를 정하여 A = g^a (mod p)를 Bob에게 전송한다.
Bob이 현재 가지고 있는 것 : g, p, A
Bob은 1<=b<=p-1을 만족하는 적당한 수 b를 정해 B = g^b (mod p)를 Alice에게 전송한다.
Alice가 현재 가지고 있는 것 : g, p, B
---------------
Alice는 Bob이 보낸 B를 a제곱하여 아래의 식을 계산한다.

Bob 또한 Alice가 보낸 A를 b제곱하여 아래의 식을 계산한다.

a와 b의 값이 매우 크지만... 앞에서 소개한 2-1 모듈로 연산에서의 거듭제곱, squeare and multiply을 이용하면 쉽게 K의 값을 구할 수 있다.
결론적으로, Alice와 Bob은 계산한 K를 통신의 키로 사용하게 된다.
공격자는 둘 사이의 통신을 도청하여 아래의 값들을 알아낼 수 있다.
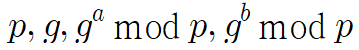
그러나 이산 로그 문제의 어려움으로.. a와 b를 알아내는 것은 불가능..
a와 b를 못구하니까 K를 구하는 것도 불가능.. ㅠ
결론적으로 이 알고리즘을 이용하면 Alice와 Bob은 모두에게 공개된 통신 채널을 이용하여도 서로 안전하게 키 교환을 할 수 있다!
4. Diffie-Hellman에 대한 중간자 공격
- 네트워크의 특성 : 네트워크로 통신하는 두 주체는 서로의 신원을 확인하기 어려움
- 중간자 공격(Man In The Middle attack, MTM)은 네트워크의 이러한 특성을 이용
- 중간자는 통신을 도청하면서 중간에 데이터를 위변조 가능
등장인물 : Alice, bob, 공격자
Alice와 Bob이 통신할 때, 공격자는 Alice에게 자신을 Bob이라고, 그리고 Bob에게는 자신을 Alice라고 속인다.
Alice와 Bob은 그냥 감쪽같이 속는다..ㅇㅅㅇ

Alice가 Bob에게 키 교환을 시도
공격자는 이를 가로채어 둘 모두와 키 교환을 진행
-> Alice는 K1, Bob은 K2 라는 키를 각각 획득
공격자에게 속은 Alice와 Bob은 공격자가 아닌 서로와 키 교환을 했다고 철썩같이 믿고 있음
Alice ---- K1로 암호화된 데이터 전송... -------->공격자는 이를 복호화하고 K2로 다시 암호화하여 전송... --------> Bob
Bob이 Alice에게 데이터 전송할 때도 마찬가지..
이 과정에서 공격자는 Alice와 Bob 사이에 오가는 정보를 모두 알 수 있으며 필요하면 이를 변조도 가능하다.
이런 취약점 때문에, Diffie-Hellan 키 교환은 서로의 신원을 확인할 수 있는 추가적인 메커니즘이 동반되어야 안전하게 이뤄질 수 있다.
최근에는 Diffie-Hellam 알고리즘이 더욱 뛰어난 성능을 보여주는 타원 곡선 Diffie-Hellman(Elliptic-Curve Diffie-Hellman. ECDH) 알고리즘으로 발전하였다고 한다..!
다음 주제는 RSA일듯